Working with complex numbers in Free Pascal.
The core of the Free Pascal programming language does not include complex numbers, however, FPC's default runtime library includes the unit uComplex, that defines the type Complex, operator overloading for this type, and lots of complex number functions. The "u" in uComplex stands for the Greek letter μ, meaning "micro", as the implementation is kept as simple as possible.
The type Complex is defined as a record of two real numbers, the first one being the real part, the second one
being the imaginary part of the complex number.
type
Complex = record
re: Real;
im: Real;
end;
PComplex = ^Complex;
The unit also defines two constants, one for the complex number i (0 + 1i), the other for the complex number 0 (0 + 0i):
const
i: Complex = (re: 0.0; im: 1.0);
_0: Complex = (re: 0.0; im: 0.0);
To assign a value to a variable of type Complex, you can assign its real and imaginary parts to the record items. Another way is to use the
function CInit:
function CInit(Zre, Zim: Real): Complex;
Arithmetic operators, as well as the equality comparison operator (=) are overloaded for usage with complex numbers; a mixture
of complex and real numbers is also possible. Some examples:
Z := Z1 + Z2;
Z := Z3 * (Z1 - Z2);
Z := Z1 ** R;
Z := Z1 ** Z2;
if Z1 = Z2 then
...
With the constant i being defined, operator overloading allows the direct assignment of a value to a complex variable,
the value being given as an arithmetic expression of the form Zre ± Zim*i. Examples:
Z := -i;
Z := 2-3*i;
The uComplex unit doesn't include any procedures for complex number input/output. There is, however, a function to convert a complex number into a string, that may
be used in a Write or Writeln statement to output the complex number.
function CStr(Z: Complex): string;
function CStr(Z: Complex; Len: Integer): string;
function CStr(Z: Complex; Len, Dec: Integer): string;
The following program sample shows some arithmetic operations and the usage of the CStr function.
program cplx1;
{$mode objfpc}{$H+}
uses
UComplex;
var
R: Real;
Z1, Z2, Z3, Z4: Complex;
begin
R := -1 / 5;
Z1 := i; Z2 := -i;
Z3 := 1 + i; Z4 := 1 - i;
Writeln('(1+i) + (1-i) = ', CStr(Z3 + Z4));
Writeln('(1+i) + (1-i) = ', CStr(Z3 + Z4, 0, 0));
Writeln('(1+i) - (1-i) = ', CStr(Z3 - Z4, 0, 0));
Writeln('-5 * [-(i-1)] = ', CStr(R * -Z4, 0, 2));
Writeln('i^2 = ', CStr(Z1 ** 2, 0, 0));
Writeln('(-i)^2 = ', CStr(Z2 ** 2, 0, 0));
Writeln;
Write('Hit ENTER to terminate '); Readln;
end.
Here is the program output:
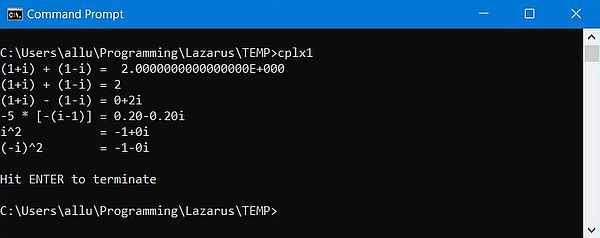 |
As you can see on the screenshot, the implementation of CStr is rudimentary. If the complex actually is a real number (if the imaginary part is zero), the number is sometimes printed as such, but sometimes is printed with ending +0i, or even -0i. Similarly, numbers that have a real part of zero are printed with leading 0+ or 0-. Even tough the programmer has well the possibility to take control over the number of decimal digits, the insignificant zeros are not dropped (but this isn't the case for the function Str either).
I just don't like such "ugly looking output". That's the reason why I have written the function ComplexToStr, that properly transforms a complex number into a string. Here is the code:
function ComplexToStr(CplxNumber: Complex): string;
// As a difference with "CStr" of the UComplex unit, this function returns a properly formatted string representation of a complex number
// Important: Real/imaginary values with an absolute value < 1E-7 are considered to be 0!
var
L: Integer;
SComplex, SReal, SImag: string;
begin
// Complex z = 0: return '0'
if (Abs(CplxNumber.Re) < 1E-7) and (Abs(CplxNumber.Im) < 1E-7) then
SComplex := '0'
// Complex z <> 0: return formatted string
else begin
// Round real and decimal part to 7 digits and remove all non-significant zeros
Str(CplxNumber.Re:0:7, SReal); Str(Abs(CplxNumber.Im):0:7, SImag);
L := Length(SReal);
while SReal[L] = '0' do
Dec(L); // non-significant zeros
if SReal[L] = '.' then
Dec(L); // decimal separator (without fractional digits)
SReal := LeftStr(SReal, L);
L := Length(SImag);
while SImag[L] = '0' do
Dec(L);
if SImag[L] = '.' then
Dec(L);
SImag := LeftStr(SImag, L);
SComplex := '';
// Keep real part only if it is <> 0
if Abs(CplxNumber.Re) >= 1E-7
SComplex := SReal;
// Keep imaginary part only if <> 0
if Abs(CplxNumber.Im) >= 1E-7 then begin
// Complex with real and imaginary part <> 0
if Abs(CplxNumber.Re) >= 1E-7 then begin
if CplxNumber.Im < 0 then
SComplex += '-'
else
SComplex += '+';
end
// Complex with imaginary part only <> 0
else begin
if CplxNumber.Im < 0 then
SComplex += '-' // minus sign has to be displayed (plus sign has not)
end;
if Abs(CplxNumber.Im) <> 1 then // use "i" instead of "1i"
SComplex += SImag;
SComplex += 'i';
end;
end;
Result := SComplex;
end;
Important: As comparing the content of a real variable to some value rarely yields an equality, all comparisons of "real/imaginary value = 0" are implemented as "absolute value of real/imaginary value ≥ 1e-7". This results in proper display of complex numbers with only a real, or only an imaginary part. On the other hand, a real/imaginary value that is less than 1e-7 will be treated as 0! Thus, if your program uses such small values, you'll have to change the code of the function...
The same program sample as before, but using the function ComplexToStr to format the complex numbers display gives the following output:
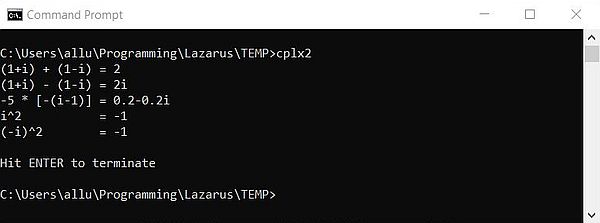 |
The uComplex unit doesn't include any function to convert a string into a complex number. I have written the function StrToComplex for this purpose. The function supposes that the string is a correctly formatted complex number string, where "correctly formatted" means with a format as the return value of the ComplexToStr function (in particular, no spaces are permitted as separators of the operator between the real and the imaginary part of the complex number). Here is the code:
function StrToComplex(SNumber: string): Complex;
// The string is supposed to be properly formatted (as the one returned by the ComplexToStr function)
var
Sign, P: Integer;
NumberRe, NumberIm: Real;
begin
if SNumber = 'i' then
SNumber := '1i'
else if SNumber = '-i' then
SNumber := '-1i';
// Complex number contains an imaginary part
if RightStr(SNumber, 1) = 'i' then begin
SNumber := LeftStr(SNumber, Length(SNumber) - 1);
Sign := 1;
// This "-" is the sign of the real part (if this one <> 0) or the sign of the imaginary part (if there is no real part)
if LeftStr(SNumber, 1) = '-' then begin
SNumber := RightStr(SNumber, Length(SNumber) - 1);
Sign := -1;
end;
// This "+" resp. "-" sign starts the imaginary part; if both are absent, the real part = 0 (cf. ComplexToStr function)
P := Pos('+', SNumber);
if P = 0 then
P := Pos('-', SNumber);
if P = 0 then begin
NumberRe := 0; Val(SNumber, NumberIm); NumberIm *= Sign;
end
else begin
Val(LeftStr(SNumber, P - 1), NumberRe); NumberRe *= Sign;
Val(RightStr(SNumber, Length(SNumber) - P + 1), NumberIm);
end;
end
// Complex number contains no imaginary part
else begin
Val(SNumber, NumberRe); NumberIm := 0;
end;
Result := CInit(NumberRe, NumberIm);
end;
The following program sample asks the user for two complex numbers and calculates their product. User input, supposed to be a correctly formatted complex number string is converted into complex numbers using StrToComplex. The product of the two numbers is displayed using ComplexToStr.
program cplx3;
{$mode objfpc}{$H+}
uses
SysUtils, Crt, UComplex;
var
S: string;
Key: Char;
Z1, Z2: Complex;
{ Convert string to complex number }
function StrToComplex(SNumber: string): Complex;
...
{ Convert complex number to string }
function ComplexToStr(CplxNumber: Complex): string;
...
begin
repeat
Writeln;
Write('Enter complex number z1? '); Readln(S);
Z1 := StrToComplex(S);
Write('Enter complex number z2? '); Readln(S);
Z2 := StrToComplex(S);
Writeln('z1 * z2 = ', ComplexToStr(Z1 * Z2));
Write('ESC to terminate, any other key to continue...');
Key := ReadKey;
if Key = #0 then
Key := ReadKey;
until Key = #27;
end.
Here is an example of the program output:
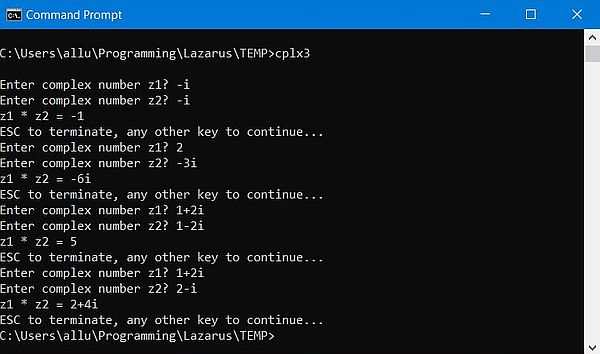 |
A complex number's conjugate, modulus (absolute value), reciprocal (inverse) and argument ("phase" φ) are returned by the following functions:
function Cong(Z: Complex): Complex;
function CMod(Z: Complex): Real;
function CInv(Z: Complex): Complex;
function CArg(Z: Complex): Real;
For a definition and the formulas to calculate these values, please, have a look at the Complex number article in Wikipedia.
The following are the complex equivalents of the standard Free Pascal real functions:
function CSqr(Z: Complex): Complex;
function CSqrt(Z: Complex): Complex;
function CExp(Z: Complex): Complex;
function CLn(Z: Complex): Complex;
The following complex trigonometric functions and inverse complex trigonometric functions are declared in uComplex:
function CCos(Z: Complex): Complex;
function CSin(Z: Complex): Complex;
function CTg (Z: Complex): Complex;
function CArc_cos(Z: Complex): Complex;
function CArc_sin(Z: Complex): Complex;
function CArc_tg(Z: Complex): Complex;
Note that CTg returns the complex tangent (not, as it may perhaps seem, the cotangent)!
And here are the declared complex hyperbolic functions and their inverse:
function CCh(Z: Complex): Complex;
function CSh(Z: Complex): Complex;
function CTh(Z: Complex): Complex;
function CArg_ch(Z: Complex): Complex;
function CArg_sh(Z: Complex): Complex;
function CArg_th(Z: Complex): Complex;
Programs on my site that deal with complex numbers.
The command line programs eququad and equcub calculate the roots of a quadratic (2nd degree) resp. cubic (3rd degree) equation with real coefficients (the roots of such equations may be complex numbers). Whereas equcub uses uComplex, eququad uses a custom record type to describe complex numbers. Click the following link to visit the Quadratic equations in one variable documentation page, and the following one to view the Cubic equations in one variable documentation.
The command line programs equcplx and equcplx2 calculate the roots of a linear (1st degree) resp. quadratic (2nd degree) equation with complex coefficients. The programs use uComplex, as well as my custom functions StrToComplex and ComplexToStr. Click the following link to visit the First degree complex equations in 1 variable documentation page, and the following one to view the Second degree complex equations in 1 variable documentation.
The command line program cplxroots calculates the nth roots of a complex number. The program doesn't use uComplex, but declares a custom record type TComplex to describe complex numbers. The input is done by entering the real and imaginary part separately. The display form of the roots may be chose by the user: standard (Cartesian) form: z=a+bi, polar form: z=r[cos(φ)+sin(φ)], or exponential form: z=reφi. Click the following link to visit the Roots of a complex number documentation page.
The GUI application Arithmetic6 is a math trainer (exercise generator) concerning the basic operations with complex numbers. The application uses uComplex, as well as my custom functions StrToComplex and ComplexToStr. Click the following link to visit the Mathematics trainer: Basic complex numbers arithmetic documentation page.
The GUI application SimpleCplxCalculator is a simple calculator application for complex numbers. Besides the 4 basic operations (+, -, x, :), it includes buttons to calculate the square, the cube, the inverse, and the modulus of a complex number. The application uses uComplex, as well as my custom functions StrToComplex and ComplexToStr. Click the following link to visit the Simple complex numbers calculator documentation page.
If you find this text helpful, please, support me and this website by signing my guestbook.