Learning: Mathematics and Science

Resistors and capacitors in series and in parallel.

This tutorial, intended for beginners, shows how to calculate the equivalent resistance resp. the equivalent capacitance of electronics circuits with 2 or more resistors resp. capacitors connected in series or in parallel.

Note: In some books and on some Inter sites, you will find the expression "total resistance" instead of the expression "equivalent resistance" used in this tutorial.

Resistors connected in series.

Resistors connected in series are connected in a head-to-tail fashion, thus forming a line or series of resistors. Calculating the equivalent resistance of the circuit may be considered as forming an equivalent circuit, where all resistors in series are replaced by a single equivalent resistor, as shown for 3 resistors on the figure below.

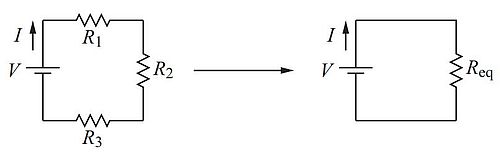So, how do we do to determine R_eq, knowing the values of R₁, R₂, and R₃? Here are the facts that we actually know:

1. Ohm's law tells us that the voltage equals the current multiplied by the resistance, that the current flows through: V = I·R.
2. In a series circuit, the total voltage equals the sum of the individual voltages, dropped at each of the resistors: V = V₁ + V₂ + V₃.
3. In a series circuit, the current through each of the resistors is the same and equal to the total current: I = I₁ = I₂ = I₃.

Applying Ohm's law to the individual resistors, and considering that the current through the 3 resistors is the same and equal to I, the second equation may be written as:

  V = I·R₁ + I·R₂ + I·R₃
    = I·(R₁ + R₂ + R₃)
    = I·R_eq

Thus, R_eq = R₁ + R₂ + R₃.

What is true for 3 resistors, remains true for any number of resistors. Thus:

The equivalent resistance of N resistors connected in series equals the sum of the individual resistances.

The same as a formula:

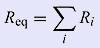Resistors connected in parallel.

Resistors connected in parallel are connected in a head-to-head and tail-to-tail fashion. The expression "in parallel" is due to the fact that such resistors are often drawn in parallel lines. The figure below shows a circuit with 3 resistors in parallel, and its equivalent circuit with one single resistor replacing the 3 individual resistors.

Here are the facts that we know in this case:

1. Ohm's law tells us that the voltage equals the current multiplied by the resistance, that the current flows through: V = I·R.
2. In a parallel circuit, the total current equals the sum of the individual currents through each of the resistors: I = I₁ + I₂ + I₃.
3. In a parallel circuit, the voltage dropped at each of the resistors is the same and equal to the total voltage: V = V₁ = V₂ = V₃.

Applying Ohm's law to the individual resistors, and considering that the voltage through the 3 resistors is the same and equal to V, the second equation may be written as:

  I = V/R₁ + V/R₂ + V/R₃
    = V/(1/R₁ + 1/R₂ + 1/R₃)
    = V/R_eq

Thus, 1/R_eq = 1/R₁ + 1/R₂ + 1/R₃.

What is true for 3 resistors, remains true for any number of resistors. Thus:

The inverse of the equivalent resistance of N resistors connected in parallel equals the sum of the inverse of the individual resistances.

The same as a formula:

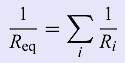To note that in a circuit with resistors connected in parallel, the equivalent resistance is always smaller than the smallest of the individual resistances.

Special case: If the circuit is made of N resistors which have all the same resistance, the equivalent resistance equals the individual resistance value divided by N.

Calculating the equivalent resistance of two resistors connected in parallel is a very frequent task. It's normally done using a simplified formula, obtained from the following calculation:

  1/R_eq = 1/R₁ + 1/R₂
        = R₁/(R₁·R₂) + R₂/(R₁·R₂)
        = (R₁+R₂) / (R₁·R₂)

Thus:

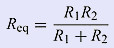Exercise.

For the circuit shown in the figure below, calculate the current that flows through the resistor R4. [Answer: 2.6 mA]

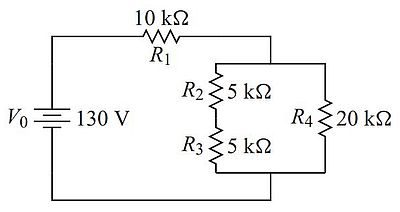Capacitors connected in parallel.

Capacitors connected in parallel are connected in a head-to-head and tail-to-tail fashion. The figure below shows a circuit with 3 capacitors in parallel, and its equivalent circuit with one single capacitor replacing the 3 individual capacitors.

Facts that we know:

1. When a voltage V is applied to a capacitor, a charge Q, depending on the capacitor's capacitance C, is stored on each plate of the capacitor: Q = C·V.
2. In a series circuit, the voltage dropped at each of the capacitors is the same and equal to the total voltage: V = V₁ = V₂ = V₃.
3. By definition, the current is the time derivative of the charge: I = dQ/dt.
4. As in a parallel circuit I = I₁ + I₂ + I₃, the total charge equals the sum of the individual charges: Q = Q₁ + Q₂ + Q₃.

Applying the first equation to each of the three capacitors, and considering that the voltage through the 3 capacitors is the same and equal to V, the last equation may be written as:

  Q = C₁·V + C₂·V + C₃·V
    = V·(C₁ + C₂ + C₃)
    = V·C_eq

Thus, C_eq = C₁ + C₂ + C₃.

What is true for 3 capacitors, remains true for any number of capacitors. Thus:

The equivalent capacitance of N capacitors connected in parallel equals the sum of the individual capacitances.

The same as a formula:

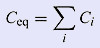Capacitors connected in series.

Capacitors connected in series are connected in a head-to-tail fashion. The figure below shows a circuit with 3 capacitors in series, and its equivalent circuit with one single capacitor replacing the 3 individual capacitors.

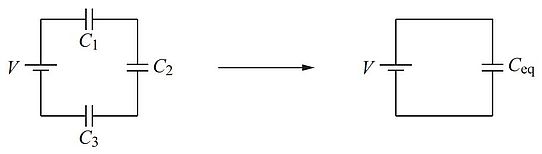Facts that we know:

1. When a voltage V is applied to a capacitor, a charge Q, depending on the capacitor's capacitance C, is stored on each plate of the capacitor: Q = C·V.
2. In a series circuit, the total voltage equals the sum of the voltages dropped at each of the capacitors: V = V₁ + V₂ + V₃.
3. By definition, the current is the time derivative of the charge: I = dQ/dt.
4. As in a parallel circuit I = I₁ = I₂ = I₃, the total charge equals the sum of the individual charges: Q ≡ Q₁ = Q₂ = Q₃ (by charge conservation).

Applying the first equation to the individual capacitors, and considering that the charge of the 3 capacitors is the same and equal to C, the second equation may be written as:

  V = Q/C₁ + Q/C₂ + Q/C₃
    = Q/(1/C₁ + 1/C₂ + 1/C₃)
    = Q/C_eq)

Thus, 1/C_eq = 1/C₁ + 1/C₂ + 1/C₃.

What is true for 3 capacitors, remains true for any number of capacitors. Thus:

The inverse of the equivalent capacitance of N capacitors connected in series equals the sum of the inverses of the individual capacitances.

The same as a formula:

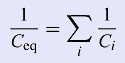Note: Inductors combine the same way that resistors do.

---

If you find this tutorial helpful, please, support me and this website by signing my guestbook.