Windows 64-bit assembly programming by example: 1. Numbers and arrays.
| Introduction | 1. Numbers and arrays | Sample programs list |
Before viewing the first program sample, lets review some important concepts concerning memory and numbers.
All data used in our assembly programs will be stored in memory (RAM), that may be seen as a sequence of 1-byte storage locations. These storage locations are referenced by a (memory) address, that is a double-word (32-bit) value, that identifies the location where the data is stored.
Numbers, handled by the x64 CPU, are essentially of two types: integers and floating point. Integers may have a size of 1 byte, 2 bytes (word), 4 bytes (double-word), or 8 bytes (quad-word). This means that a given integer value may use more than one memory location. If, for example, we store a double-word to address x, then this value will occupy memory locations x, x+1, x+2, and x+3. It's always the lowest address that is used to reference the value in memory, thus, to load our double word into a register, we must execute a move instruction, with x as source operand.
On a 64-bit platform, it is normally the best (at least the easiest) way to use quad-word data. This avoids a lot of possible problems with not working code, and you can't see what you did wrong.
If our integers are unsigned (all positive) integers, or if they are signed integers (positive or negative), depends on the programmer. As we will use functions of the C library for input-output, we have the possibility to use the "%u" format for unsigned integers, and the "%d" format for signed integers. Remember, that in the binary system, negative numbers are numbers with the most significant bit set to 1. They are obtained by determining the two's complement of the positive equivalent. Example: binary representation of -5. Binary 5 is given by 0000000000000101. Changing all 0 into 1 and vice-versa, we obtain: 1111111111111010. Finally, adding 1, binary -5 is 1111111111111011, or hexadecimal FFFB.
We said above, that our double-word stored at address x will occupy memory locations x through x+3. But, how are the 4 bytes making up the number will actually be stored? Will address x contain the first (MSB) byte, or will it contain the last one (LSB)? On Intel CPUs, that are part of the so-called little-endian CPUs, it's the LSB that is stored at x! This may appear confusing and complicated. But, in reality, it's not a big deal. In fact, in normal situations, we haven't to care about this. When we store the content of a double-word register to memory, it will be stored in the correct way, and when we reload it into a double-word register, it will be loaded correctly.
The internal representation of floating point numbers is more complicated than the one of integers, and this topic falls out the scope of this tutorial. Lets just remember that single precision floats have a size of 4 bytes (double-word), double precision floats a size of 8 bytes (quad-word).
With the understanding of memory storage locations and numbers, we can now view how to deal with arrays of numbers (most of the program samples of the tutorial actually use arrays). In higher programming languages, an array is a sequence of elements of the same data type. Individual array elements can be accessed using an index. Languages like Pascal allow to use indexes of data types like characters or enumerations. In most cases, however, indexes are integer values, and normally the first element of the array has an index of 0, what defines an index range from 0 .. N - 1, where N is the number of elements of the array.
In assembly an array is referenced by its base address, what actually is the address of the first array element. With an array of bytes, things are quite simple. If x is the base address of the array, than the first element is stored at address x (x + 0), the second at address x + 1, the third as address x + 2, etc. The difference between the address of a given element and the base address of the array is called offset. In our byte array, the fifth element would have an offset of 5 - 1 = 4, the last element would have an offset of N - 1.
If the data type of the array elements is more than 1 byte in size, things become a little more complicated. Lets consider an array of double-words. If the base address of the array is x, the first array element would be stored in a memory area corresponding to the addresses x through x + 3, the second element in a memory area x + 4 through x + 7, the third in a memory area x + 8 through x + 11. If we calculate the offsets we get the values 0 (first element), 4 (second element), 8 (third element), etc. The offsets actually are multiples of 4, and 4 bytes actually is the size of the array values.
From what is said above, we can deduce how to access a given element of the array. We can, for example, use direct memory addressing mode, what means that we specify the element offset within the "move" (or other) instruction. For example, with our double-word example from before, the instruction mov [x+12], eax will copy the content of register EAX to the fourth element of the array with base address x.
To access all values of an array in sequential order, we use indirect memory addressing mode. Before we start to iterate the array, we load an index register with the base address of the array. Then during each iteration, we add a value equal to the data type size to the content of the index register, that thus points to the next array element.
Another way to iterate through the array elements consists in loading the array base address in one register (ex: RDX), and during each iteration, increment the index of the array element stored in another register (ex: RCX, initialized to 0 before starting the iteration loop). The value of the array element with its index equal to the actual content of RCX can then be accessed using the indirect addressing mode operand [rdx + rcx*s] (s being the size in bytes of the array values data type).
Sorry for this rather long theoretical introduction. But, I think that explaining these fundamental concepts all together and before starting with the sample programs, is more adequate than explaining a part of it with one sample and another with the next one. Anyway, array iteration and element addressing will be reviewed in the explanations of the samples where they are used.
Concerning the sample code, displayed on this page, please, note that the numbers at the line beginnings aren't part of the assembly code, but references that I use in the explanations following the code. If you want, you can click the following link and download the source code of the samples of Numbers and arrays part of the tutorial.
Sample 1: Maximum of an array of unsigned integers.
The program maximum.asm takes an array of 10 positive integers (defined within the program) and prints out the maximum value of this array. Here is the code.
format ELF64
[001] section '.data' writeable
[002] arrlen equ 10
[003] arr dw 100, 400, 700, 200, 900, 300, 800, 600, 500, 400
[004] frmat db "Maximum value in array: %u", 0Dh, 0Ah, 0
[005] section '.text' executable
[006] public main
[007] extrn printf
[008] main:
[009] push rbp
[010] mov rbp, rsp;
[011] sub rsp, 32
[012] and rsp, -16
[013] mov cl, arrlen - 1
[014] lea esi, [arr]
[015] xor rax, rax
[016] mov word ax, [esi]
[017] next:
[018] add esi, 2
[019] mov word bx, [esi]
[020] cmp ax, bx
[021] jge continue
[022] mov ax, bx
[023] continue:
[024] dec cl
[025] cmp cl, 0
[026] jne next
[027] mov rdx, rax
[028] mov rcx, frmat
[029] call printf
[030] mov rsp, rbp
[031] pop rbp
[032] xor rax, rax
[033] ret
[003]:
The declaration of an initialized array of unsigned integers is done using one of the pseudo-instructions db,
dw, dd, dq, followed by the values of the array elements (words, in our case), separated by commas.
[004]:
This line defines the output format to be used with the C function printf (cf. a book about the C programming language, if you need
help). Note the usage of %u, that means an unsigned integer.
[013] - [016]:
Register initialization before entering the iteration loop. We load the index register ESI with the address of the array; i.e.
ESI points initially to the array's first element. We will use AX to store the maximum. At this point, we suppose that it corresponds to the first element's value, thus
we store the value, that ESI points to, into AX (to be sure that the upper bytes of the 64-bit register RAX are 0, we clear RAX before doing the
mov instruction). The register CL is used as a counter. As the loop will start with the second array element, the number of iterations is equal
to the number of elements - 1.
[017] - [026]:
The iteration loop, actually not more difficult to code in assembly than in a higher programming language. Adding 2 (the size of
a word) to ESI, the index register points to the next array element, that we load into register BX. If the value in AX is greater than the value in BX, the value in AX
remains the correct maximum value; if AX is less than BX, BX is the new maximum value, and we store its content into AX. In both cases, we decrement the counter in CX.
Unless it is 0 (all elements processed), we continue with the next array element.
[027] - [029]:
Output of the maximum. When printing out one value with printf, we have to give the function two
arguments: 1. the output format; 2. the value. Argument passing in Windows 64-bit assembly is done using the registers RCX, RDX, ... So, we load RCX with the address of
the format, and RDX with the maximum calculated (in RAX). Then we call the external function printf.
Sample 2: Minimum of an array of signed integers.
The program minimum.asm takes an array of 20 signed (positive or negative) integers (defined within the program) and prints out the minimum value in this array. The program is fundamentally the same as the one before (except that we have to test if the actual minimum is less or equal than the new array element, in order to continue without replacing the minimum). However, our array contains signed integers, so can (and does) contain negative numbers. In binary notation, a negative number has its most significant bit set to 1. As the value of the minimum is passed to printf in RDX (a 64-bit register), this actually is bit 63. The numbers we are dealing with have thus to be 64-bit integers (qwords)! Here is the code of minimum.asm.
format ELF64
[001] section '.data' writeable
[002] arrlen equ 20
[003] arr dq 1, -4, -7, 2, -9, 3, -3, -6, 0, 6, 5, -1, 4, 7, -2, 9, -5, 8, -8, 0
[004] frmat db "Minimum value in array: %d", 0Dh, 0Ah, 0
[005] section '.text' executable
[006] public main
[007] extrn printf
[008] main:
[009] push rbp
[010] mov rbp, rsp;
[011] sub rsp, 32
[012] and rsp, -16
[013] mov cl, arrlen - 1
[014] lea esi, [arr]
[015] mov qword rax, [esi]
[016] next:
[017] add esi, 8
[018] mov qword rbx, [esi]
[019] cmp rax, rbx
[020] jle continue
[021] mov rax, rbx
[022] continue:
[023] dec cl
[024] cmp cl, 0
[025] jne next
[026] mov rdx, rax
[027] mov rcx, frmat
[028] call printf
[029] mov rsp, rbp
[030] pop rbp
[031] xor rax, rax
[032] ret
[003]:
The declaration of an initialized array of signed integers is done using the pseudo-instruction dq. Using
64-bit values makes sure that negative numbers are handled correctly.
[004]:
The symbol in the format argument of the C function printf for signed integers is %d.
[013] - [015]:
Register initialization is as in the program before: array address into ESI, first array element value into RAX (64-bit
register!), counter in CL.
[016] - [025]:
The iteration loop is similar as in the program before. However, as the array elements are qwords, we have to add 8 to ESI in
order to make it point to the next element. Also, we have to use the 64-bit register RBX instead of BX. And, of course, the conditional jump jge
continue of the maximum program (line 21) has to be changed to jle continue in the minimum program (line 20).
[026] - [028]:
The code for the output of the minimum is the same as in the program before.
Sample 3: Minimum and maximum of an array of signed integers.
The program minmax.asm takes an array of 20 signed (positive or negative) integers (defined within the program) and prints out the minimum and maximum value in this array. The new assembly topic that we'll learn about in this sample, is the usage of functions.
In assembly, a function is an independent block of code, placed behind the main program code. It is identified by a label (that may be seen as the function name), and terminates with the instruction ret that returns control to the caller (main program or other function). To call a function (i.e. execute the code within the function block), the instruction call <function-name> is used.
In the program samples of this tutorial, there has no care been taken to follow any conventions or standard rules. I pass the function arguments using custom registers, 64-bit or others. Maybe that this is not best practice. But, I don't see why I couldn't do it; if the subroutine input and output is documented (using comments), everyone will understand the code. And as these functions are only intended to be called from the sample program, that they are part of, this shouldn't be a problem. Maybe, that assembly programmers would disagree (?).
Here is the code of minmax.asm. It is made of three blocks: 1. the main program that calls first the function "min" to calculate the minimum, that it prints out, then calls the function "max" to calculate the maximum that it prints out; 2. the function "min" that calculates the minimum of an array of given length; 3. the function "max" that calculates the maximum of an array of given length.
format ELF64
[001] section '.data' writeable
[002] arrlen equ 20
[003] arr dq 1, -4, -7, 2, -9, 3, -3, -6, 0, 6, 5, -1, 4, 7, -2, 9, -5, 8, -8, 0
[004] frmat1 db "Minimum value in array: %d", 0Dh, 0Ah, 0
[005] frmat2 db "Maximum value in array: %d", 0Dh, 0Ah, 0
[006] section '.text' executable
[007] public main
[008] extrn printf
[009] main:
[010] push rbp
[011] mov rbp, rsp;
[012] sub rsp, 32
[013] and rsp, -16
[014] mov cl, arrlen
[015] lea esi, [arr]
[016] call min
[017] mov rcx, frmat1
[018] call printf
[019] mov cl, arrlen
[020] lea esi, [arr]
[021] call max
[022] mov rcx, frmat2
[023] call printf
[024] mov rsp, rbp
[025] pop rbp
[026] xor rax, rax
[027] ret
[028] ;
[029] ; Minimum value of an array of signed integers
[030] ;
[031] ; Input: ESI: Pointer to array
[032] ; CL: Number of array elements
[033] ; Output: RDX: Minimum
[034] min:
[035] push rax
[036] mov qword rdx, [esi]
[037] dec cl
[038] minnext:
[039] add esi, 8
[040] mov qword rax, [esi]
[041] cmp rdx, rax
[042] jle mincont
[043] mov rdx, rax
[044] mincont:
[045] dec cl
[046] cmp cl, 0
[047] jne minnext
[048] pop rax
[049] ret
[050] ;
[051] ; Maximum value of an array of signed integers
[052] ;
[053] ; Input: ESI: Pointer to array
[054] ; CL: Number of array elements
[055] ; Output: RDX: Maximum
[056] max:
[057] push rax
[058] mov qword rdx, [esi]
[059] dec cl
[060] maxnext:
[061] add esi, 8
[062] mov qword rax, [esi]
[063] cmp rdx, rax
[064] jge maxcont
[065] mov rdx, rax
[066] maxcont:
[067] dec cl
[068] cmp cl, 0
[069] jne maxnext
[070] pop rax
[071] ret
[014] - [023]:
The (non-prolog-non-epilog) code of the main program. Both the min and the
max functions need two arguments: a pointer to the array (= address of the array) in ESI and the array length (= number of elements) in CL,
so we have to load these registers before calling the functions. The minimum resp maximum is returned in RDX, where it has to be for calling
printf. Before doing so, we have to load RCX with the address of the display format ("frmat1" for printing the minimum; "frmat2" for printing
the maximum).
[034] - [049]:
The "min" function that calculates the minimum of the array (of length given in CL) pointed to by ESI and returns this
minimum in the RDX register. The code is fundamentally the same than lines [015] - [025] in minimum.asm. Note, that CL has here to be decremented before entering the
loop, because its initial value has to be 1 less than the number of array elements, passed as argument (in minimum.asm, it is loaded with this value). Remains to explain
the reason for the instruction push rax in line [035]. It is used to save the RAX register that is internally used by the function, and thus
will loose its original value (there is no such value in this program sample, but it could be one if the function was used in some other program, and it's always a
good idea to save the registers that are changed by a subroutine). The original value of RAX will be restored at the end of the function, using the instruction
pop rax in line [048].
[056] - [071]:
The "max" function that calculates the maximum of the array (of length given in CL) pointed to by ESI and returns this
maximum in the RDX register. The code is fundamentally the same than lines [016] - [026] in maximum.asm. Decrement of CL for the same reason as above. The
push rax (line [057] and pop rax (line [070]) are used for the same reason as in the "min"
function.
Exercise suggestion: Rewrite the same program, but using one single call to printf.
Sample 4: Average of an array of floating-point numbers.
Floating point numbers are a rather complex topic. Lets just remember some basic facts (enough to be able to handle floating point data in our sample programs).
- Data in memory should be declared as quad-words.
- There are special registers to deal with floating-point data: registers XMM0 to XMM15. They have a size of 128 bits. XMM8 to XMM15 are accessible only in 64-bit operating mode, whereas XMM0 to XMM7 may be used with 32-bit floating point numbers (single precision), as well as 64-bit floating-point numbers (double precision).
- There are special instructions to deal with floating point data; examples: movsd instead of mov, addsd instead of add.
- Instructions with floating point registers may not be used with the immediate addressing mode; work-around: declare the constant value in the data section and use the direct addressing mode.
- Some floating point related instructions are rather complicated and weird (example: comparison of two floating point values). Either remember how to use them, or simply copy and paste the code from a working example.
The program sample average.asm calculates the average of an array of 10 floating point values (declared in the program). The program logic is quite simple: Iterate the array and at each iteration, add the element's value to the sum. When the iteration is done, divide the sum by the number of array elements. Here is the code:
format ELF64
[001] section '.data' writeable
[002] arrlen equ 10
[003] ten dq 10.0
[004] arr dq 1.5, 4.2, 7.8, 2.4, 9.1, 3.3, 8.7, 6.2, 5.4, 0.4
[005] frmat db "Average value of array: %.2f", 0Dh, 0Ah, 0
[006] section '.text' executable
[007] public main
[008] extrn printf
[009] main:
[010] push rbp
[011] mov rbp, rsp;
[012] sub rsp, 32
[013] and rsp, -16
[014] mov cl, arrlen - 1
[015] lea esi, [arr]
[016] movsd xmm0, [esi]
[017] next:
[018] add esi, 8
[019] addsd xmm0, [esi]
[020] dec cl
[021] cmp cl, 0
[022] jne next
[023] movsd xmm1, [ten]
[024] divsd xmm0, xmm1
[025] movq rdx, xmm0
[026] mov rcx, frmat
[027] call printf
[028] mov rsp, rbp
[029] pop rbp
[030] xor rax, rax
[031] ret
[003]:
As we may not use immediate addressing with floating point registers, we declare the number of array elements as variable; make sure to declare it as a
floating point value (10.0, and not 10)!
[004]:
The declaration of a double precision number is done using the pseudo-instruction dq. This is also the case
for the declaration of an initialized double precision array, where the array elements (separated by commas) follow dq.
[005]:
The symbol in the format argument of the C function printf for floating point numbers is something like
%.2f (display with 2 decimal digits).
[014] - [016]:
Register initialization before entering the iteration loop. We load the index register ESI with the address of the array (i.e.
ESI points initially to the array's first element). We will use XMM0 to store the sum. At this point, we load it with the first element's value, thus
we store the value, that ESI points to, into XMM0 (note the usage of the instruction movsd). The register CL is used as a counter. As the loop
will start with the second array element, the number of iterations is equal to the number of elements - 1.
[017] - [022]:
Iteration loop. Adding 8 (the size of a qword) to ESI, the index register points to the next array element, that we add to
the content of the XMM0 register (note the usage of the instruction addsd). Then, we decrement the counter in CX. Unless it is 0 (all elements
processed), we continue with the next array element.
[023] - [024]:
Average calculation. What we have to do is dividing the sum of the array elements (actually in XMM0) by the element number.
The instruction divsd has two register operands, the first one being the dividend, the second one being the divisor, and the result of the
division being put into the destination (i.e. the first) operand. So, we first load the register XMM1 with the floating point value 10.0 (value taken from memory; direct
addressing mode), then divide the content of XMM0 by the content of XMM1 (with the result, i.e. the average) in XMM0.
[025] - [027]:
Average output. We pass the arguments to the C function printf in the same way as we did in the
samples before: the display format in RCX, the value to display in RDX. As the average actually is in XMM0, we have to load RDX with the content of XMM0. This is done
using the special move instruction movq.
Sample 5: Minimum and maximum of an array of floating-point numbers.
The program sample minmax2.asm does exactly the same than sample minmax.asm, but here the array elements are floating point numbers (instead of integers). The only really new topic that we learn with this sample is the comparison of two floating point numbers. Here is the code:
format ELF64
[001] section '.data' writeable
[002] arrlen equ 20
[003] arr dq 1.5, -5.5, 4.2, -2.4, -6.8, 7.8, 2.4, -0.7, 9.5, 3.3, -1.7, -4.4, 8.7, 6.2, -7.7, -0.1, 5.4, 0.4, -9.5, -6.6
[004] frmat1 db "Minimum value in array: %.2f", 0Dh, 0Ah, 0
[005] frmat2 db "Maximum value in array: %.2f", 0Dh, 0Ah, 0
[006] section '.text' executable
[007] public main
[008] extrn printf
[009] main:
[010] push rbp
[011] mov rbp, rsp;
[012] sub rsp, 32
[013] and rsp, -16
[014] mov cl, arrlen
[015] lea esi, [arr]
[016] call min
[017] movq rdx, xmm0
[018] mov rcx, frmat1
[019] call printf
[020] mov cl, arrlen
[021] lea esi, [arr]
[022] call max
[023] movq rdx, xmm0
[024] mov rcx, frmat2
[025] call printf
[026] mov rsp, rbp
[027] pop rbp
[028] xor rax, rax
[029] ret
[030] ;
[031] ; Minimum of an array of floating point numbers
[032] ;
[033] ; Input: ESI: Pointer to array
[034] ; CL: Number of array elements
[035] ; Output: XMM0: Minimum
[036] ; Registers: XMM1 and XMM2 are changed!
[037] min:
[038] push rax
[039] movsd xmm0, [esi]
[040] dec cl
[041] minnext:
[042] add esi, 8
[043] movsd xmm1, [esi]
[044] movsd xmm2, xmm1
[045] cmpnltsd xmm2, xmm0
[046] movd eax, xmm2
[047] test eax, eax
[048] jnz mincont
[049] movsd xmm0, xmm1
[050] mincont:
[051] dec cl
[052] cmp cl, 0
[053] jne minnext
[054] pop rax
[055] ret
[056] ;
[057] ; Maximum of an array of floating point numbers
[058] ;
[059] ; Input: ESI: Pointer to array
[060] ; CL: Number of array elements
[061] ; Output: XMM0: Maximum
[062] ; Registers: XMM1 and XMM2 are changed!
[063] max:
[064] push rax
[065] movsd xmm0, [esi]
[066] dec cl
[067] maxnext:
[068] add esi, 8
[069] movsd xmm1, [esi]
[070] movsd xmm2, xmm1
[071] cmplesd xmm2, xmm0
[072] movd eax, xmm2
[073] test eax, eax
[074] jnz maxcont
[075] movsd xmm0, xmm1
[076] maxcont:
[077] dec cl
[078] cmp cl, 0
[079] jne maxnext
[080] pop rax
[081] ret
[014] - [025]:
The (non-prolog-non-epilog) code of the main program. Both the min and the
max functions need two arguments: a pointer to the array (= address of the array) in ESI and the array length (= number of elements) in CL,
so we have to load these registers before calling the functions. The minimum resp maximum is returned in XMM0. To print out these values, we use the C function
printf, with the display format (depending on what we print) having to be in RCX, and the value to be displayed in RDX. To move the
maximum/minimum (content of XMM0) to RDX, we use the special move instruction movq.
[037] - [055]:
The "min" function that calculates the minimum of the array (of length given in CL) pointed to by ESI and returns this
minimum in the XMM0 register. This code corresponds to lines [034] - [047] in minmax.asm. The logic is exactly the same. As here we are dealing with floating point numbers,
we use XMM0 (actual minimum) and XMM1 (iteration element) instead of RDX and RAX. And, of course, we have to use the floating point instructions, in particular
movsd instead of mov. To compare the actual minimum with the actual iteration element, we'll have to
compare the content of two floating point registers (XMM0 and XMM1). However, the destination operand of this compare is modified (cf. further
down), thus we copy XMM1 to XMM2, and use XMM2 instead of XMM1 in the comparison instruction. The instruction cmpnltsd xmm2,
xmm0 checks if the content of XMM2 is not less than (i.e. is greater or equal than) the content of XMM0 (the value of the actual element is greater or equal
than the actual minimum). The instruction will leave 0 or all 1 bits in the destination register XMM2 (this is the modification of the destination that I mentioned before)
to represent false or true. To branch based on the result of floating point compare operations, you should move the destination register into a general
purpose register and then test that register for zero/not zero. In our case, we move XMM2 to EAX, test EAX and branch if the result of the test is not zero. i.e.
when the comparison result was true, what means here that the content of XMM2 was "not less than" (i.e. was greater or equal) than the content of XMM0, and the minimum
value has not to be adapted (the instruction movsd xmm0, xmm1 is skipped). I agree, this is somewhat weird and not necessarily easy to understand.
But, as I said above, if you don't get it, just copy the code from a working program to your new one...
[063] - [081]:
The "max" function that calculates the maximum of the array (of length given in CL) pointed to by ESI and returns this
maximum in the XMM0 register. This code corresponds to lines [054] - [067] in minmax.asm. As above, we use XMM0 (actual maximum) and XMM1 (iteration element) instead of
RDX and RAX. To compare the actual maximum with the actual iteration element, we'll have to compare the content of two floating point registers
(XMM0 and XMM1). As the destination operand of this compare is modified, we copy XMM1 to XMM2, and use XMM2 instead of XMM1 in the comparison instruction. The instruction
cmplesd xmm2, xmm0 checks if the content of XMM2 is less or equal than the content of XMM0 (the value of the actual
element is less or equal than the actual maximum). To branch based on this compare operation, we move XMM2 into EAX, then test EAX. If the result of the test is not zero,
i.e. if the comparison result was true, what means here that the content of XMM2 was less or equal than the content of XMM0, and the maximum value has not to be adapted,
branch, skipping the instruction movsd xmm0, xmm1.
Note: This subroutine changes the registers RAX, XMM1, and XMM2. RAX is preserved (saved to and restored from the stack), whereas the floating point registers will have to be saved by the caller if they contain some value that must not be overwritten by the subroutine (an arbitrary choice to do so, primarily because there is no instruction to push a floating point register onto the stack).
Exercise suggestion: Rewrite the same program, but using one single call to printf.
Sample 6: Squares of the elements of an array of unsigned integers.
The sample program squares.asm prints out an array of 20 positive integers (declared within the program), and then calculates and prints out the elements' squares. As a difference with the samples before, where at each iteration we added the size of the array data type to ESI, we use here an element index (ECX) and at each iteration, we compute the offset by adding this index multiplied by the length of the array data type to the array base address in ESI.
format ELF64
[001] section '.data' writeable
[002] arrlen equ 20
[003] arr dw 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20
[004] count dq 0
[005] frmat db "%3u ", 0
[006] eol db 0Dh, 0Ah, 0
[007] section '.text' executable
[008] public main
[009] extrn printf
[010] main:
[011] push rbp
[012] mov rbp, rsp;
[013] sub rsp, 32
[014] and rsp, -16
[015] mov rcx, 0
[016] print1:
[017] cmp rcx, arrlen
[018] je continue
[019] xor rax, rax
[020] mov word ax, [arr+rcx*2]
[021] inc rcx
[022] mov [count], rcx
[023] mov rcx, frmat
[024] mov rdx, rax
[025] call printf
[026] mov rcx, [count]
[027] jmp print1
[028] continue:
[029] mov rcx, eol
[030] call printf
[031] mov rcx, 0
[032] print2:
[033] cmp rcx, arrlen
[034] je done
[035] xor rax, rax
[036] mov word ax, [arr+rcx*2]
[037] imul ax
[038] inc rcx
[039] mov [count], rcx
[040] mov rcx, frmat
[041] mov rdx, rax
[042] call printf
[043] mov rcx, [count]
[044] jmp print2
[045] done:
[046] mov rsp, rbp
[047] pop rbp
[048] xor rax, rax
[049] ret
[015]:
Initialization of the register RCX, that will be used as counter of the array elements processed within the iteration loops. The content of RCX, starting at
0, and incremented by 1 at each iteration, corresponds to the element index in higher programming languages, and will not only be used to
terminate the loop, but also to calculate the offset of the array elements, needed to calculate the element's address.
[016]-[027]:
First iteration loop: For each array element, display its value. The array indices are form 0 to array length - 1, so we quit
the loop when the content of RCX has reached a value equal to the array length (number of array elements). We then load the actual element into AX. The array elements
being declared as words, we use a 16-bit register, and the offset of the actual element equals the array index (in RCX) multiplied by 2 (element size). The address
of the actual element is obtained by adding the offset to the array base address: [arr+rcx*2]. We then increment the element counter (index),
and save its new to some memory location ("temporary variable"). Now we can set the registers for the call of printf: display format to RCX,
actual element (in RAX) to RDX. Finally, we restore the RCX register and jump for the next iteration step.
[028]-[031]:
The array elements have been displayed one behind the other, so we have to print out a CR/LF now (to go to a new line before displaying the square
values). Then we reset RCX to 0 for the second iteration loop.
[032]-[044]:
Second iteration loop: For each array element, calculate the square and display it. The code is exactly the same as the one of
the first loop, except the supplementary line [037], where we use the imul instruction to multiply the content of RAX by itself (calculation
of the square).
Maybe, you wonder why in the first loop I use RAX that I then copy to RDX, and not directly RDX (for the C print-out the array element has to be in RDX). Simply because I wanted to have "the same code" in both loops. And in the second loop, we must use RAX, as multiplication (as well as division) only work with the accumulator registers.
Sample 7: Squares of the elements of an array of unsigned integers (with "squares" subroutine).
The sample program squares2.asm does the same as squares.asm, but this time, we use a "squares" subroutine that calculates the squares of the array elements. It's an example that shows the usage of pointers to pass an array to a subroutine and modify an array passed to a subroutine. Also note, that in this sample both the increment of ESI (in the subroutine) and the usage of an element index (in the main program) are used to access the array elements.
format ELF64
[001] section '.data' writeable
[002] arrlen equ 20
[003] arr dw 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20
[004] count dq 0
[005] frmat db "%3u ", 0
[006] eol db 0Dh, 0Ah, 0
[007] section '.bss' writeable
[008] arr2 dw 20 dup (?)
[009] section '.text' executable
[010] public main
[011] extrn printf
[012] main:
[013] push rbp
[014] mov rbp, rsp;
[015] sub rsp, 32
[016] and rsp, -16
[017] lea esi, [arr]
[018] lea edi, [arr2]
[019] mov cl, arrlen
[020] call square
[021] mov rcx, 0
[022] print1:
[023] cmp rcx, arrlen
[024] je continue
[025] xor rax, rax
[026] mov word ax, [arr+rcx*2]
[027] inc rcx
[028] mov [count], rcx
[029] mov rcx, frmat
[030] mov rdx, rax
[031] call printf
[032] mov rcx, [count]
[033] jmp print1
[034] continue:
[035] mov rcx, eol
[036] call printf
[037] mov rcx, 0
[038] print2:
[039] cmp rcx, arrlen
[040] je done
[041] xor rax, rax
[042] mov word ax, [arr2+rcx*2]
[043] inc rcx
[044] mov [count], rcx
[045] mov rcx, frmat
[046] mov rdx, rax
[047] call printf
[048] mov rcx, [count]
[049] jmp print2
[050] done:
[051] mov rsp, rbp
[052] pop rbp
[053] xor rax, rax
[054] ret
[055] ;
[056] ; Squares of the elements of an array of unsigned integers
[057] ;
[058] ; Input: ESI: Pointer to original array
[059] ; EDI: Pointer to squares array
[060] ; CL: Number of array elements
[061] ; Output: The squares array will be filled
[062] square:
[063] push rax
[064] push rbx
[065] mov bl, 0
[066] next:
[067] cmp bl, cl
[068] je square_end
[069] mov word ax, [esi]
[070] imul ax
[071] mov word [edi], ax
[072] add esi, 2
[073] add edi, 2
[074] inc bl
[075] jmp next
[076] square_end:
[077] pop rbx
[078] pop rax
[079] ret
[007]-[008]:
The declaration of an uninitialized array of unsigned integers is done using one of the pseudo-instructions db, dw, dd, dq,
followed by a number N and dup (?). This means that a memory area of N * {integer-size}, in other words {array-size} * {integer-size} is reserved.
The (?) tells the assembler that the array is not initialized at program start. Uninitialized data has to be declared in the
.bss section.
[017]-[020]:
Calculation of the squares by calling the subroutine "square". This subroutine requires three
arguments: 1. a reference to the source array (original values) in ESI; 2. a reference to the destination array (squares) in EDI; 3. the array length (number of elements)
in CL. So, we load these registers before making the call. When returning from the subroutine, the destination array will be filled with the square values.
[021]:
Setting the element counter RCX (also used as array index) to 0 before entering the iteration loop.
[022]-[033]:
First iteration loop: Display of the original array elements. The element address is calculated by adding the offset
rcx*2 to the base address of the original array ("arr"). All this is identical to what we did in the sample program
before.
[035]-[037]:
Display of a CR/LF (in order to pass to a new line for the display of the squares), and reset the element counter to 0 for the second iteration loop.
[038]-[049]:
Second iteration loop: Display of the squares. The element address is calculated by adding the offset
rcx*2 to the base address of the squares array ("arr2"). For the rest, all identical to the code above.
[062]-[079]:
Subroutine to calculate the squares. At subroutine entry, ESI contains the address of the first element of the original array,
EDI the address of the first element of the squares array, and CL the array length (the same for both arrays, of course). Before entering the iteration loop, we set
BL, that will be used as element counter, to 0. If the value in BL equals the one in CL, all elements have been processed, and we quit the loop. Otherwise, we take the
value at the memory location pointed to by ESI (original array element), multiply it by itself (to compute the square), then store it to the memory location pointed to by
EDI. We then increment ESI and EDI by 2 (the array elements are words), thus pointing them to the next element. Finally we increment the element counter, and start
processing the next array element. As RAX and RBX are changed, we save these two registers when entering the subroutine, and restore the original values before returning
to the caller.
Exercise suggestion: Write a program with identical layout to calculate the squares of an array of floating point numbers (or, if you think that that is to difficult, try with signed integers first).
Sample 8: Squares of the elements of an array of unsigned integers (with "display" subroutine).
The sample program squares3.asm does the same as squares.asm and squares2.asm, but this time, we use a subroutine to print out the arrays. As sample squares2.asm, it shows how to use pointers in order to pass an array to a subroutine. The new topic, that you will learn with this example is the extra instructions, that you have to insert within the code of a subroutine in order to satisfy the 64-bit calling convention when calling an external function like printf in our case.
format ELF64
[001] section '.data' writeable
[002] arrlen equ 20
[003] arr dw 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20
[004] frmat db "%3u ", 0
[005] eol db 0Dh, 0Ah, 0
[006] section '.bss' writeable
[007] arr2 dw 20 dup (?)
[008] savcnt dq ?
[009] savarr dq ?
[010] savlen dq ?
[011] section '.text' executable
[012] public main
[013] extrn printf
[014] main:
[015] push rbp
[016] mov rbp, rsp;
[017] sub rsp, 32
[018] and rsp, -16
[019] mov rcx, 0
[020] next:
[021] cmp rcx, arrlen
[022] je continue
[023] mov word ax, [arr+rcx*2]
[024] imul ax
[025] mov word [arr2+rcx*2], ax
[026] inc rcx
[027] jmp next
[028] continue:
[029] mov rcx, arrlen
[030] lea rdx, [arr]
[031] call print_arr
[032] mov rcx, arrlen
[033] lea rdx, [arr2]
[034] call print_arr
[035] mov rsp, rbp
[036] pop rbp
[037] xor rax, rax
[038] ret
[039] ;
[040] ; Display all elements of an array of unsigned integers
[041] ;
[042] ; Input: RCX: Array length
[043] ; RDX: Array base address
[044] ; Output: -----
[045] ; Functions: printf (external C function)
[046] ;
[047] print_arr:
[048] sub rsp, 32
[049] push rax
[050] push rbx
[051] mov rbx, 0
[052] print:
[053] cmp rbx, rcx
[054] je print_arr_end
[055] xor rax, rax
[056] mov word ax, [rdx+rbx*2]
[057] inc rbx
[058] mov [savlen], rcx
[059] mov [savcnt], rbx
[060] mov [savarr], rdx
[061] mov rcx, frmat
[062] mov rdx, rax
[063] call printf
[064] mov rcx, [savlen]
[065] mov rbx, [savcnt]
[066] mov rdx, [savarr]
[067] jmp print
[068] print_arr_end:
[069] mov rcx, eol
[070] call printf
[071] pop rbx
[072] pop rax
[073] add rsp, 32
[074] ret
[006]-[010]:
The .bss section is used to declare uninitialized variables, in our case the square array (as in the program before), and 3
variables that our "print" procedure will use to temporarily save some qword values. To declare an uninitialized qword, use the pseudo-instruction
dq followed by a question mark.
[019] - [038]:
The (non-prolog-non-epilog) code of the main program. At line [019], we reset RCX, that is used as element counter and index,
before entering the squares calculation loop (lines [020] - [027]). We then print out the original array (lines [029] - [031]) and the squares array (lines [032] - [034]).
Print out is done, calling our custom subroutine "print_arr", that requires 2 arguments: the array length in RCX, and the array base address
("arr" for the original array, "arr2" for the squares array) in RDX.
[047] - [074]:
The "print_arr" subroutine, described in detail in the following paragraphs.
[048] / [073]:
The magic lines required in all subroutines that make a call to another subroutine following the 64-bit calling convention.
The instruction sub rsp, 32 reserves 32 bytes of shadow space, what is absolutely mandatory when we call
printf. The reservation of shadow space requires the reset of the stack pointer before leaving the subroutine. This
is done in line [073] using the instruction add rsp, 32. If you forget the magic lines, your program will crash!
[049] - [050]:
Backup of the used registers RAX (used to retrieve the different array elements while iterating the loop), and RBX (used as
element counter (array index).
[051]:
Reset of the element counter RBX (before entering the iteration loop).
[052] - [067]:
Iteration loop: Iterating the array elements from first to last and printing out their values. First, we check if RBX (the
element counter) equals RCX (number of array elements); if so, we quit the loop (remember that array elements are counted from 0 to length - 1). Second, we load the actual
element into RAX; this element's address is given by RDX (array base address) + RCX (array index) multiplied by 2 (array elements size). Third, we increment RBX (the
array index). In lines [058] - [060], we save the content of RBX, RCX, and RDX to the .bss, then in lines [061] - [063] we print out the actual array element. Before
processing the next element (jumping to "print"), we restore RBX, RCX, and RDX from the .bss.
[069] - [070]:
When all array elements have been printed out, we print the end of line characters CR+LF in order to move the cursor to a
new line.
[071] - [072]:
Restore of the used registers RAX and RBX.
Sample 9: Sort of an array of unsigned integers.
The sample program bubble.asm performs a simple bubble sort on an array of 20 positive integers declared within the program. The original array and the sorted array are displayed using a subroutine.
format ELF64
[001] section '.data' writeable
[002] arrlen equ 20
[003] arr dw 400, 700, 200, 450, 900, 300, 800, 100, 150, 650, 250, 950, 850, 350, 550, 600, 500, 400, 750, 200
[004] frmat db "%3u ", 0
[005] eol db 0Dh, 0Ah, 0
[006] section '.bss' writeable
[007] savcnt dq ?
[008] savarr dq ?
[009] savlen dq ?
[010] section '.text' executable
[011] public main
[012] extrn printf
[013] main:
[014] push rbp
[015] mov rbp, rsp;
[016] sub rsp, 32
[017] and rsp, -16
[018] mov rcx, arrlen
[019] lea rdx, [arr]
[020] call print_arr
[021] mov cl, 0
[022] lea esi, [arr]
[023] outer:
[024] mov edi, esi
[025] add edi, 2
[026] mov dl, cl
[027] inc dl
[028] inner:
[029] mov word ax, [esi]
[030] mov word bx, [edi]
[031] cmp ax, bx
[032] jle continue
[033] mov [esi], bx
[034] mov [edi], ax
[035] continue:
[036] add edi, 2
[037] inc dl
[038] cmp dl, arrlen
[039] jl inner
[040] add esi, 2
[041] inc cl
[042] cmp cl, arrlen - 1
[043] jl outer
[044] mov rcx, arrlen
[045] lea rdx, [arr]
[046] call print_arr
[047] mov rsp, rbp
[048] pop rbp
[049] xor rax, rax
[050] ret
[039] ;
[051] ; Display all elements of an array of unsigned integers
[052] ;
[053] ; Input: RCX: Array length
[054] ; RDX: Array base address
[055] ; Output: -----
[056] ; Functions: printf (external C function)
[057] ;
[058] print_arr:
[059] sub rsp, 32
[060] push rax
[061] push rbx
[062] mov rbx, 0
[063] print:
[064] cmp rbx, rcx
[065] je print_arr_end
[066] xor rax, rax
[067] mov word ax, [rdx+rbx*2]
[068] inc rbx
[069] mov [savlen], rcx
[070] mov [savcnt], rbx
[071] mov [savarr], rdx
[072] mov rcx, frmat
[073] mov rdx, rax
[074] call printf
[075] mov rcx, [savlen]
[076] mov rbx, [savcnt]
[077] mov rdx, [savarr]
[078] jmp print
[079] print_arr_end:
[080] mov rcx, eol
[081] call printf
[082] pop rbx
[083] pop rax
[084] add rsp, 32
[085] ret
[018]-[020]:
Display of the original array. This is done by calling the procedure "print_arr", with 2
arguments: the number of elements in RCX, and a pointer to the array in RDX.
[021]-[043]:
The bubble sort code. It's a "translation into assembly" of the following Pascal code:
for I := 0 to Length(Arr) - 2 do begin
for J := I + 1 to Length(Arr) - 1 do begin
if Arr[I] > Arr[J] then begin
A := Arr[I]; Arr[I] := Arr[J]; Arr[J] := A;
end;
end;
end;
Detailed explanations follow below...
[021]-[022]:
Initialization before entering the double loop: The register CL will be used as counter of the outer loop variable
(this corresponds to the variable I in the Pascal code) and is here set to 0. The register ESI is used to point to the array element used with the outer loop counter
(this corresponds to the array element Arr[I] in the Pascal code) and is set here to point to the first array element.
[023]-[027]:
First part of the outer loop. It initializes the inner loop counter DL (this corresponds to the variable J in the Pascal code),
and the EDI register, used to point to the array element used with the inner loop (this corresponds to the array element Arr[J] in the Pascal code). At the beginning of a
new inner loop iteration, the inner loop counter is set to the outer loop counter + 1 (I + 1 -> J; CL + 1 -> DL). The inner loop array element has to be the one following
the outer loop element. In Pascal, this is automatically the case for J = I + 1. In assembly, we have to increment EDI, taking the array data type length into
consideration. As the array elements have been declared as words, this length is 2 bytes, that's why we have: ESI + 2 -> EDI.
[028]-[039]:
The inner loop. With the outer loop array element (Arr[I] in Pascal) being always the same, the inner loop array element
(Arr[J] in Pascal) varies by iteration. For each inner loop element, we check if the outer element is less or equal. If yes, the elements are in ascending order and we
can simply continue. If the outer loop element is however greater than the inner loop element, then the two elements have to be swapped (lines [033] - [034]). In both
cases, we are then ready to process the next inner loop element. EDI has to be incremented by 2 (as the data is of type word), the inner loop counter DL is incremented by
1. If, after increment DL is still less than the number of array elements, we continue looping (lines [037] - [039]); otherwise the inner loop is terminated.
[040]-[043]:
Second part of the outer loop. The actual outer loop element (Arr[I] in Pascal) has been compared to all inner loop elements
(Arr[J] in Pascal) that we want to compare it with, and we are ready to process the next outer loop element. ESI has to be incremented by 2 (as the data is of type word),
the outer loop counter CL is incremented by 1. If, after increment, CL is still less than the number of array elements - 1, we continue looping (lines [041] - [043]);
otherwise the outer loop is terminated.
[044]-[046]:
Display of the now sorted array by calling the subroutine "print_arr".
[058]-[085]:
The array display subroutine. It's exactly the same code as in the program sample squares3.asm.
Sample 10: Sort of an array of signed integers entered by the user.
All our sample programs so far have used data that is defined within the source code. This new sample will use data, entered from the keyboard. We will use the C function scanf to read the data.
The sample bubble2.asm reads a series of signed integers from the keyboard, input continuing until the number 0 is entered (this number is considered not to be part of the series). The numbers entered are stored into an array, that is printed out, then sorted and printed out again. Data input, data output, and data sorting are coded with subroutines. Here is the code:
format ELF64
[001] section '.data' writeable
[002] maxlen equ 50
[003] asktxt db "Enter a series of integers, terminated by 0", 0Dh, 0Ah, 0
[004] asknum db "? ", 0
[005] frmatin db "%lli", 0
[006] frmat db "%lli ", 0
[007] eol db 0Dh, 0Ah, 0
[008] section '.bss' writeable
[009] array dq 50 dup (?)
[010] arrlen dq ?
[011] num dq ?
[012] savlen dq ?
[013] savlen2 dq ?
[014] savcnt dq ?
[015] savarr dq ?
[016] section '.text' executable
[017] public main
[018] extrn printf
[019] extrn scanf
[020] main:
[021] push rbp
[022] mov rbp, rsp;
[023] sub rsp, 32
[024] and rsp, -16
[025] mov rcx, asktxt
[026] call printf
[027] mov rcx, maxlen
[028] lea rdx, [array]
[029] call array_input
[030] cmp rax, 2
[031] jl main_end
[032] mov [arrlen], rax
[033] mov rcx, [arrlen]
[034] lea rdx, [array]
[035] call array_print
[036] mov rcx, [arrlen]
[037] lea rdx, [array]
[038] call array_sort
[039] mov rcx, [arrlen]
[040] lea rdx, [array]
[041] call array_print
[042] main_end:
[043] mov rsp, rbp
[044] pop rbp
[045] xor rax, rax
[046] ret
[047] ;
[048] ; Enter a series of signed integers from the keybord and
[049] ; store these numbers into an array. Input is terminated
[050] ; by entering 0 (this 0 will not be included in the array)
[051] ;
[052] ; Input: RCX: Maximum array length
[053] ; RDX: Array base address
[054] ; Output: RAX: Actual array length
[055] ; The array will be filled with the numbers entered
[056] ; Functions: printf, scanf (external C functions)
[057] ;
[058] array_input:
[059] sub rsp, 32
[060] mov [savlen], rcx
[061] mov [savarr], rdx
[062] mov rcx, 0
[063] .input_next:
[064] cmp rcx, [savlen]
[065] je array_input_end
[066] mov [savcnt], rcx
[067] mov rcx, asknum
[068] call printf
[069] mov rcx, frmatin
[070] mov rdx, num
[071] call scanf
[072] mov rax, [num]
[073] cmp rax, 0
[074] je array_input_end
[075] mov rcx, [savcnt]
[076] mov rdx, [savarr]
[077] mov [rdx+rcx*8], rax
[078] inc rcx
[079] jmp .input_next
[080] array_input_end:
[081] mov rax, [savcnt]
[082] add rsp, 32
[083] ret
[084] ;
[085] ; Display all elements of an array of signed integers
[086] ;
[087] ; Input: RCX: Array length
[088] ; RDX: Array base address
[089] ; Output: -----
[090] ; Functions: printf (external C function)
[091] ;
[092] array_print:
[093] sub rsp, 32
[094] push rax
[095] push rbx
[096] mov rbx, 0
[097] .print:
[098] cmp rbx, rcx
[099] je array_print_end
[100] mov rax, [rdx+rbx*8]
[101] inc rbx
[102] mov [savlen], rcx
[103] mov [savcnt], rbx
[104] mov [savarr], rdx
[105] mov rcx, frmat
[106] mov rdx, rax
[107] call printf
[108] mov rcx, [savlen]
[109] mov rbx, [savcnt]
[110] mov rdx, [savarr]
[111] jmp .print
[112] array_print_end:
[113] mov rcx, eol
[114] call printf
[115] pop rbx
[116] pop rax
[117] add rsp, 32
[118] ret
[119] ;
[120] ; Sort an array of signed integers
[121] ;
[122] ; Input: RCX: Array length
[123] ; RDX: Array base address
[124] ; Output: -----
[125] ; The array elements will be sorted
[126] ;
[127] array_sort:
[128] mov [savlen], rcx
[129] dec rcx
[130] mov [savlen2], rcx
[131] mov rsi, rdx
[132] mov rcx, 0
[133] .sort_outer:
[134] mov rdi, rsi
[135] add rdi, 8
[136] mov rdx, rcx
[137] inc rdx
[138] .sort_inner:
[139] mov rax, [rsi]
[140] mov rbx, [rdi]
[141] cmp rax, rbx
[142] jle .sort_continue
[143] mov [rsi], rbx
[144] mov [rdi], rax
[145] .sort_continue:
[146] add rdi, 8
[147] inc rdx
[148] cmp rdx, [savlen]
[149] jl .sort_inner
[150] add rsi, 8
[151] inc rcx
[152] cmp rcx, [savlen2]
[153] jl .sort_outer
[154] array_sort_end:
[155] ret
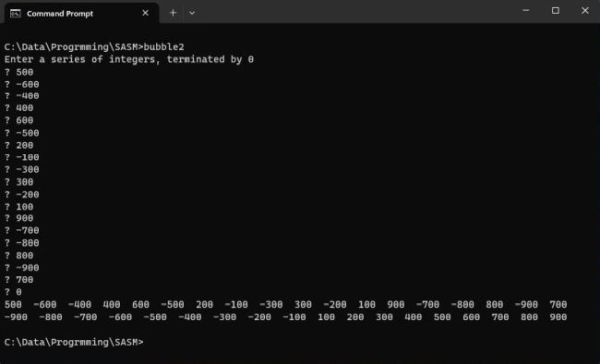
The screenshot below shows the output of bubble2.exe.
|
[025]-[026]:
Display "number input text", making a call to the printf function.
[027]-[032]:
Number input, making a call to the "array_input" function. This function requires 2 arguments:
the maximum array length (arbitrarily fixed at 50) in RCX, and the base address of the array, where the numbers entered will be stored, in RDX. The function returns the
actual array length (number of integers entered by the user). If this number is less than 2, no need to make a sort (program termination). Note, that the array length
is saved to "[arrlen]" for later usage.
[033]-[035]:
Display of the original array, making a call to the "array_print" subroutine. This subroutine
requires 2 arguments: the array length in RCX, and the base address of the array in RDX.
[036]-[038]:
Sort of the array, making a call to the "array_sort" subroutine. This subroutine also requires 2
arguments: the array length in RCX, and the base address of the array in RDX (when returning from the subroutine, the original values of the array elements will be
replaced by the sorted values).
[039]-[041]:
Display of the sorted array, making a call to the "array_print" subroutine.
[058]-[083]:
The "array_input" function, detailed below.
[059]:
The call to the C functions printf and scanf makes it necessary to define some shadow
space.
[060]-[062]:
Initialization before entering the input loop. The maximum array length and the array base address are temporarily saved to
the .bss. The register RCX, used as array element counter is set to 0.
[064]-[071]:
If the array element counter (RCX) equals the maximum number of elements, we terminate user input. Otherwise we ask the user to enter
an integer number. After having saved RCX, we display a question mark, then make a call to the C function scanf.
This function has here 2 arguments: First the input format ("%lli" is used for 64-bit integers), that has to be loaded into the RCX register,
second the address where the input should be stored; at this point, we store it to a temporary memory area in the .bss ("[num]").
[072]-[077]:
Storage of the number entered into the array. We first check if the number entered is 0; in this case, user input is terminated.
Otherwise, we restore the actual array element counter (into RAX) and the array base address (into RDX) from the .bss and use them to calculate the actual array element's
address: [rdx+rcx*8] (multiplier 8, because the array elements are qwords).
[078]-[079]:
We increment the number of array elements and continue with the next user input.
[081] - [082]:
Exit of the function: We store the actual number of array elements (i.e. the function return) into RAX. Important not to
forget to reset the stack pointer before returning to the calling program!
[092]-[118]:
The "array_print" subroutine. This subroutine has been described before. One important note however:
the line mov word ax, [rdx+rbx*2] in program sample 9 (where the array elements were words) has to be changed here to
mov rax, [rdx+rbx*8], because our array data type is quad-word!
[127]-[155]:
The "array_sort" subroutine. The bubble sort code is essentially the same as the one used in the
sample 9 main program. For detailed explanations, see below.
[128]-[132]:
Initialization before entering the double loop. First, we save the array length and the array length minus 1 (this value will be
needed in the outer loop compare operation) to the .bss. Then, we load RSI (used to point to the outer loop array element) with the array base address, passed to the
routine in RDX, and set the outer loop counter (RCX) to 0.
[133]-[137]:
First part of the outer loop. We load RDI (used to point to the inner loop array element) with the address of the element
following the one referred to by RSI (as the array elements are qwords, we have to add 8 bytes), and set the inner loop counter (RDX) to RCX + 1.
[138]-[149]:
The inner loop. With the outer loop array element being always the same, the inner loop array element varies by iteration.
For each inner loop element, we check if the outer element is less or equal. If yes, the elements are in ascending order and we can simply continue. If the outer loop
element is however greater than the inner loop element, then the two elements have to be swapped (lines [143] - [144]). In both cases, we are then ready to process the
next inner loop element. RDI has to be incremented by 8 (as the data is of type qword), the inner loop counter RDX is incremented by 1. If, after the increment, RDX is
still less than the number of array elements, we continue looping (lines [147] - [149]); otherwise the inner loop is terminated.
[150]-[153]:
Second part of the outer loop. The actual outer loop element has been compared to all inner loop elements that we want to
compare it with, and we are ready to process the next outer loop element. RSI has to be incremented by 8 (as the data is of type word), the outer loop counter RCX is
incremented by 1. If, after the increment, RCX is still less than the number of array elements - 1 (we stored this value into "[savlen2]") at
the beginning of the procedure), we continue looping (lines [151] - [153]); otherwise the outer loop is terminated and we return to the calling program.
Note: I guess that you have noticed that in the sort routine of this program, I use RSI and RDI (instead of ESI and EDI). This is because of the array base address passed in RDX, that is a 64-bit register...
Exercise suggestion: Change the sort routine in order to make it possible to either sort in ascending or descending order; in the main program, ask the user which sorting order they want.
Sample 11: Usage of two-dimensional arrays.
The next sample program shows how to access given elements of a two-dimensional array in assembly. To learn to understand how two-dimensional arrays are handled in assembly, lets consider a Pascal array of the form A: array[0..3, 0..3] of Char. This array contains 16 bytes organized as four rows of four characters. Somehow, we’ve got to draw a correspondence with each of the 16 bytes of this array and 16 contiguous bytes in main memory.
The actual mapping is not important as long as two conditions are satisfied: (1) each element maps to a unique memory location (that is, no two entries in the array occupy the same memory locations) and (2) the mapping is consistent (that is, a given element in the array always maps to the same memory location). So, what we need is a function with two input parameters (row and column) that produces an offset into a linear array of 16 memory locations. While a large number of possible functions fit this bill, two functions in particular are used by most programmers and high-level languages: row-major ordering and column-major ordering.
Row-major ordering assigns successive elements, moving across the rows and then down the columns, to successive memory locations, as shown on the figure below. It's this function that we will use in this tutorial.
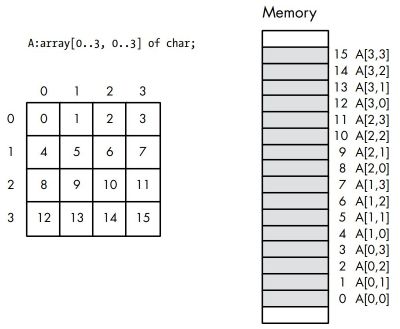
|
Lets take for example the array elements [1, 2] and [2, 1], located in column 3 of row 2, and column 2 of row 3 respectively. On the figure, we can see that this corresponds to offsets of 6 and 9 respectively. How these offsets are calculated? Simply by multiplying the row index by 4 and adding the column index: 1*4 + 2 = 6; 2*4 + 1 = 9. General formula to calculate the offset of an array element of given data type length, located at a given row- and column-index of an array with given number of columns:
| offset = (row-index * number-of-columns + column-index) * data-type-length |
This is demonstrated in the program sample matrix_element.asm, that prints out two given elements of a 3x4 matrix (declared in the program).
format ELF64
[001] section '.data' writeable
[002] rows equ 3
[003] cols equ 4
[004] dsize equ 2
[005] matrix dw 0, 1, 2, 3
[006] dw 10, 11, 12, 13
[007] dw 20, 21, 22, 23
[008] frmat1 db "Matrix element M[1, 2] = %u", 0Dh, 0Ah, 0
[009] frmat2 db "Matrix element M[2, 1] = %u", 0Dh, 0Ah, 0
[010] section '.text' executable
[011] public main
[012] extrn printf
[013] main:
[014] push rbp
[015] mov rbp, rsp;
[016] sub rsp, 32
[017] and rsp, -16
[018] mov rax, 1
[019] mov rbx, 2
[020] mov rcx, cols
[021] mov rdx, dsize
[022] call element_offset
[023] mov rcx, frmat1
[024] xor rdx, rdx
[025] mov word dx, [matrix+rax]
[026] call printf
[027] mov rax, 2
[028] mov rbx, 1
[029] mov rcx, cols
[030] mov rdx, dsize
[031] call element_offset
[032] mov rcx, frmat2
[033] xor rdx, rdx
[034] mov word dx, [matrix+rax]
[035] call printf
[036] mov rsp, rbp
[037] pop rbp
[038] xor rax, rax
[039] ret
[040] ;
[041] ; Calculate two dimensional arry element offset
[042] ;
[043] ; Input: RAX: Row-index
[044] ; RBX: Column-index
[045] ; RCX: Number of columns in array
[046] ; RDX: Size of elements data type
[047] ; Output: RAX: element offset
[048] element_offset:
[049] push rdx
[050] imul rcx
[051] add rax, rbx
[052] pop rdx
[053] imul rdx
[054] ret
[018]-[026]:
Print out of array element [1, 2]. We load the registers RAX - RDX with the values that have to be passed as arguments to
the "element_offset" function. This function returns the element's offset in RAX; thus the address of the element to be printed is RAX added
to the array base address. This value has to be loaded into RDX (the format for the first element's print out in RCX) in order to call printf.
[027]-[035]:
Print out of array element [2, 1]. Same as before, except for the index values to be loaded into RAX and RBX.
[048]-[054]:
The "element_offset" function calculates the element's offset using the formula seen above. With the function's
arguments in RAX - RDX: offset = (RAX * RCX + RBX) * RDX. Do you see why I pushed the RDX register at the begin of the subroutine and restored it before
using its content (data type size) in the offset calculation? Here is a hint: If I don't do it, all array elements will be displayed as being 0. Still not found the reason?
It's because of the first imul instruction. With the 64-bit multiplication instructions, the first operand is always RAX, and the result is
RAX for the 64 LSB bits and RDX for the 64 MSB bits (all 0 in our case).
Sample 12: Addition of 2 matrices.
The program sample matrix_add.asm adds two 2x2 matrices and prints out the sum matrix. Here is the code:
format ELF64
[001] section '.data' writeable
[002] rows equ 2
[003] cols equ 2
[004] dsize equ 8
[005] matrix1 dq 100, 200
[006] dq -200, -100
[007] matrix2 dq 100, -100
[008] dq 100, -100
[009] frmat db "%4Li ", 0
[010] eol db 0Dh, 0Ah, 0
[011] section '.bss' writeable
[012] srow dq ?
[013] scol dq ?
[014] section '.text' executable
[015] public main
[016] extrn printf
[017] main:
[018] push rbp
[019] mov rbp, rsp;
[020] sub rsp, 32
[021] and rsp, -16
[022] mov rax, 0
[023] next_row:
[024] cmp rax, rows
[025] je done
[026] mov rbx, 0
[027] next_col:
[028] cmp rbx, cols
[029] je continue
[030] mov [srow], rax
[031] mov [scol], rbx
[032] mov rcx, cols
[033] mov rdx, dsize
[034] call element_offset
[035] mov rdx, [matrix1+rax]
[036] add rdx, [matrix2+rax]
[037] mov rcx, frmat
[038] call printf
[039] mov rax, [srow]
[040] mov rbx, [scol]
[041] inc rbx
[042] jmp next_col
[043] continue:
[044] mov rcx, eol
[045] call printf
[046] mov rax, [srow]
[047] inc rax
[048] jmp next_row
[049] done:
[050] mov rsp, rbp
[051] pop rbp
[052] xor rax, rax
[053] ret
[054] ;
[055] ; Calculate two dimensional arry element offset
[056] ;
[057] ; Input: RAX: Row-index
[058] ; RBX: Column-index
[059] ; RCX: Number of columns in array
[060] ; RDX: Size of elements data type
[061] ; Output: RAX: element offset
[062] element_offset:
[063] push rdx
[064] imul rcx
[065] add rax, rbx
[066] pop rdx
[067] imul rdx
[068] ret
The screenshot below shows the output of matrix_add.exe.
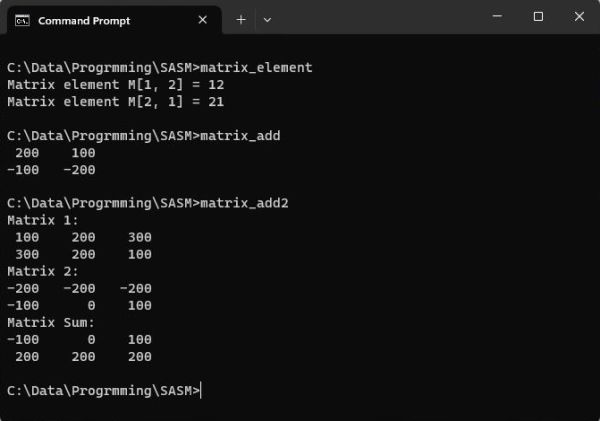
|
[022]:
Initialization of the row index (RAX), before starting the outer loop.
[023] - [026]:
First part of the outer loop (row iteration). If the row index equals the number of rows, we are done. Otherwise we proceed
with the initialization of the column index (RBX), before starting the inner loop.
[027] - [042]:
Inner loop (for each row, column iteration). If the column index equals the number of columns, we leave the loop. Otherwise,
we calculate the offset for the actual row and column indices, add the corresponding array elements and print them out. RAX and RBX already contain the correct values
for the call of "element_offset"; RCX and RDX are loaded now. When returning from the subroutine, RAX contains the offset and can be used to
access the actual elements in the two matrices in order to calculate their sum. This sum is then printed out, and after incrementing the column index RBX, we can proceed
with the next column. Note line [046], where we restore the value of RAX, saved before.
[043] - [048]:
Second part of the outer loop (row iteration). First we print an end-of-line. Then we increment the row index RAX and proceed
with the next row. Note line [030] and [031], where we temporarily save the values in RAX and RBX; their values will be restored in lines [039] and [040].
[062]-[068]:
The "element_offset" function; identical to the one used in the sample before (lines [048] - [054]).
Exercise suggestion: Addition of two matrices of floating point numbers. And if you start to like assembly and want to prove to yourself that you are meanwhile not only able to read and understand, but also to write assembly programs, why not try three-dimensional arrays? For example, calculate the sum of two or more matrices stored in an array of matrices...
Sample 13: Random number series.
Is it possible to generate random numbers in assembly, you may ask. Of course, it is! One simple possibility would for example be to call the C function rand(). On modern Intel processors, it's even easier. The Digital Random Number Generator (DRNG) is an innovative hardware approach to high-quality, high-performance entropy and random number generation. It is composed of the new Intel x64 instructions rdrand and rdseed and an underlying DRNG hardware implementation. DRNG is described in detail on the Intel website.
The DRNG may be directly accessed by an application program. Here is how rdrand, used in program samples 12 and 13, is described in Intel® 64 and IA-32 Architectures Software Developer’s Manual, Volume 1, Section 7.3.17, "Random Number Generator Instructions": "rdrand loads a hardware generated random value and stores it in the destination register. The size of the random value is determined by the destination register size and operating mode. The Carry Flag indicates whether a random value is available at the time the instruction is executed. CF=1 indicates that the data in the destination is valid. Otherwise CF=0 and the data in the destination operand will be returned as zeros for the specified width. All other flags are forced to 0 in either situation. Software must check the state of CF=1 for determining if a valid random value has been returned, otherwise it is expected to loop and retry execution of rdrand."
To load a random number into register RAX, use code like:
try_rand:
rdrand rax
jnc try_rand
The program sample random.asm generates (and displays) 100 random numbers between 1 and 99. The question now is, how to transform the random number generated into a
number in the range that we want? It's lots easier than you might think. Whatever the random number is, if we divide it by 99, the rest of this division is always a
number between 0 and 98; and if we add 1 to this rest, we'll get a number between 1 and 99, as we want it to be. Things become a little more tricky if the lower
interval is greater than 1 (e.g. random number between 10 and 20). The general formula for a random number included in the interval [nlow ; nhigh] is given by:
n = r mod (nhigh - nlow + 1) + nlow
where n is the number in the desired interval, r is the original random number (here the one returned by rdrand), mod is the modulo operator
(rest of a division), and nlow and nhigh are the minimum and maximum values in the interval considered. Lets try it out for random numbers between 10 and 20, with,
for example, r = 3444. In this case our number n would be 3447 mod (20 - 10 + 1) + 10 = 4 + 10 = 14.
Implementing the modulo function in assembly is easy. The instruction div divides the content of RAX by the destination operand, placing the integer result of the division into RAX and the rest of this division (i.e. the result of our modulo operation) into RDX. That's it!
Here is the code of the sample program random.asm.
format ELF64
[001] section '.data' writeable
[002] nums equ 100
[003] nlow equ 1
[004] nhigh equ 99
[005] count dq 0
[006] frmat db "%2llu ", 0
[007] eol db 0Dh, 0Ah, 0
[008] section '.text' executable
[009] public main
[010] extrn printf
[011] main:
[012] push rbp
[013] mov rbp, rsp;
[014] sub rsp, 32
[015] and rsp, -16
[016] mov rcx, 0
[017] next:
[018] cmp rcx, nums
[019] je done
[020] try_rand:
[021] rdrand rax
[022] jnc try_rand
[023] xor rdx, rdx
[024] mov rbx, nhigh - nlow + 1
[025] div rbx
[026] add rdx, nlow
[027] mov [count], rcx
[028] mov rcx, frmat
[029] call printf
[030] xor rdx, rdx
[031] mov rax, [count]
[032] inc rax
[033] mov rbx, 10
[034] div rbx
[035] cmp rdx, 0
[036] jne continue
[037] mov rcx, eol
[038] call printf
[039] continue:
[040] mov rcx, [count]
[041] inc rcx
[042] jmp next
[043] done:
[044] mov rcx, eol
[045] call printf
[046] mov rsp, rbp
[047] pop rbp
[048] xor rax, rax
[049] ret
The screenshot below shows the output of random.exe.
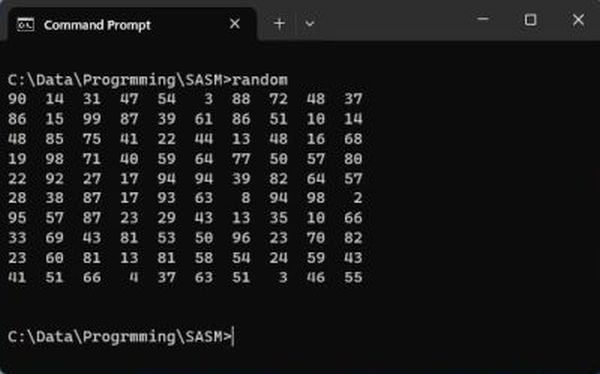
|
[016]:
Initialization of the number counter (RCX), before starting the loop.
[017] - [019]:
The first thing to do when entering the loop (iteration for each of the 100 numbers to generate and display) is to check if
all numbers have been generated; if so (as RCX is initialized with 0, this is when RCX contains 100), we leave the loop.
[020] - [022]:
Waiting for a random number being ready and storing it into the RAX register.
[023] - [026]:
Computing the corresponding number in the preset interval. This is done by dividing the original random number (RAX) by
nhigh - nlow + 1. What we are interested in is the rest of this division (RDX). Our number is obtained by adding the rest of the division to nlow.
[027]:
Saving the content of the number counter (RCX).
[028] - [029]:
Print out of the actual random number.
[030] - [038]:
This (not mandatory) code produces a formatted output of the random number series, by inserting an end-of-line after every
10 numbers displayed (cf. screenshot of the program output). How to detect "every 10th number"? Simply by dividing the number counter (loaded from the address, where we
saved it before, into the RAX register and adding 1, as we started with 0 for the first number) by 10. If the rest of this division (RDX) equals 0, another 10 numbers
have been done, and the carriage-return-linefeed has to be printed out (resp. if the rest is different from 0, we skip the print-out of the end-of-line character).
[039] - [042]:
We now prepare for the next number: Restore of the number counter into RCX, increment of the counter and jumping at the
beginning of the loop.
[043] - [045]:
Print-out of a final end-of-line character when the complete series has been displayed.
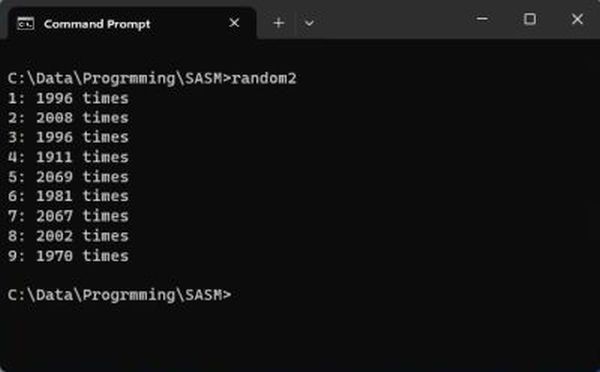
Sample 14: Random number distribution (number counts).
The program sample random2.asm generates 18,000 random numbers between 1 and 9 and counts how often each number has been generated. Here is the code:
format ELF64
[001] section '.data' writeable
[002] nums equ 18000
[003] nlow equ 1
[004] nhigh equ 9
[005] ncounts equ 9
[006] counts dq 9 dup 0
[007] count dq 0
[008] frmat db "%1llu: %4llu times", 0Dh, 0Ah, 0
[009] section '.text' executable
[010] public main
[011] extrn printf
[012] main:
[013] push rbp
[014] mov rbp, rsp;
[015] sub rsp, 32
[016] and rsp, -16
[017] mov rcx, 0
[018] rand_next:
[019] cmp rcx, nums
[020] je counts_display
[021] rand_try:
[022] rdrand rax
[023] jnc rand_try
[024] xor rdx, rdx
[025] mov rbx, nhigh - nlow + 1
[026] div rbx
[027] add rdx, nlow
[028] lea rbx, [counts]
[029] inc qword [rbx+(rdx-1)*8]
[030] inc rcx
[031] jmp rand_next
[032] counts_display:
[033] mov rcx, 0
[034] display_next:
[035] cmp rcx, ncounts
[036] je done
[037] lea rbx, [counts]
[038] inc rcx
[039] mov [count], rcx
[040] mov r8, [rbx+(rcx-1)*8]
[041] mov rdx, rcx
[042] mov rcx, frmat
[043] call printf
[044] mov rcx, [count]
[045] jmp display_next
[046] done:
[047] mov rsp, rbp
[048] pop rbp
[049] xor rax, rax
[050] ret
The screenshot below shows the output of random2.exe.
|
[017]:
Initialization of the number counter (RCX), before starting the random number generation/count loop.
[018] - [020]:
The first thing to do when entering the random number generation/count loop (iteration for each of the 18,000 numbers to
generate and count their occurrences) is to check if all numbers have been generated; if so, we leave the loop.
[021] - [023]:
Waiting for a random number being ready and storing it into the RAX register.
[024] - [027]:
Computing the corresponding number in the preset interval. This is the same code as in the previous sample (lines [023] -
[026]).
[028] - [029]:
Increment of the counter for this random number. The counters for the 9 random numbers are defined as an array with 9
elements. To calculate the address of the element to increment, we take the array base address and add the array index multiplied by the data size (8, as we use qwords).
As the counter for 1 is located at index 0, the counter for 2 at index 1, etc, the index equals the value of the random number (RDX) minus 1.
[030] - [031]:
We now prepare for the next number: Increment of the number counter and jumping at the beginning of the loop.
[032] - [033]:
When all random numbers have been generated, we pass at the initialization of the number counter (RCX), before starting the
counts display loop.
[034] - [036]:
The first thing to do when entering the counts display loop (iteration for each of the 9 random number counters) is to check
if all counts have been displayed; if so, we leave the loop.
[037] - [043]:
Display of the actual number and its count (how many times it has been generated). The address of the count for the actual
number is calculated as before, when we incremented the counters (lines [028] - [029]). The C function printf has to have 3 arguments in this
case: 1. the output format (RCX); 2. the random number (RDX); 3. the count for this random number (R8). The actual random number is obtained by incrementing the number
counter (that we initialized to 0) by 1. As RCX is needed for the output format, this (next number) counter is temporarily saved to memory in line [039].
[044] - [045]:
We now prepare for the next number: Restore of the number counter saved before (no need to increment it, as this has already
been done) and jumping at the beginning of the loop.
[046]:
When all counts have been displayed, we are ready to leave the routine.
Some "real world" programs.
The programs so far are samples to show given aspects of the x64 assembly language programming, without doing as such something really useful. The following 3 programs perform some "real" task. They are presented as example code (to study, to understand, and to inspire), without comments or explanations. I think that if you have read the previous part of this tutorial and understood the samples given, you should be able to follow the logic of the 3 programs without greater difficulties.
Sample 15: "Guess the number" game.
The sample program guess.asm is a 64-bit assembly implementation of the classic "Guess the number" game. The computer "thinks of" some number, and the player has to find it. At each guess made by the player, they are told if the guess is smaller or greater as the computer's number. Until the number has been found...
format ELF64
section '.data' writeable
nlow equ 1
nhigh equ 100
count dq 0
gtitle db 'Guess the Number game in x64 Assembly (FASM).', 0Dh, 0Ah, 0
qnumber db 'Please, enter a number between 1 and 100? ', 0
bnumber db 'Your number is to big!', 0Dh, 0Ah, 0
snumber db 'Your number is to small!', 0Dh, 0Ah, 0
enumber db 'Congratulations! You have found the number in %llu guesses.', 0Dh, 0Ah, 0
frmatin db '%llu', 0
section '.bss' writeable
rnum dq ?
unum dq ?
section '.text' executable
public main
extrn printf
extrn scanf
main:
push rbp
mov rbp, rsp;
sub rsp, 32
and rsp, -16
mov rcx, gtitle
call printf
try_rand:
rdrand rax
jnc try_rand
xor rdx, rdx
mov rbx, nhigh - nlow + 1
div rbx
add rdx, nlow
mov [rnum], rdx
next:
mov rcx, qnumber
call printf
mov rcx, frmatin
mov rdx, unum
call scanf
mov rax, [unum]
cmp rax, nlow
jl done
cmp rax, nhigh
jg done
inc qword [count]
cmp rax, [rnum]
jl toosmall
jg toobig
mov rcx, enumber
mov rdx, [count]
call printf
jmp done
toosmall:
mov rcx, snumber
call printf
jmp next
toobig:
mov rcx, bnumber
call printf
jmp next
done:
mov rsp, rbp
pop rbp
xor rax, rax
ret
The screenshot below shows the output of guess.exe.
|
Sample 16: Linear equations in one variable.
The sample program equation1.asm solves equations of the form ax + b = 0. The user is asked for the coefficients a and b; the program determines x (if it exists).
format ELF64
section '.data' writeable
dtitle db "Linear equations in one variable: ax + b = 0", 0Dh, 0Ah, 0
askparm db "Coefficients a and b? ", 0
frmatin db "%Lf%Lf", 0
droots db "This equation has a unique solution: x = %.3f", 0Dh, 0Ah, 0
dnosol db "This equation has no solutions", 0Dh, 0Ah, 0
dinfsol db "This equation has an infinity of solutions", 0Dh, 0Ah, 0
a dq 0.0
b dq 0.0
section '.text' executable
public main
extrn printf
main:
push rbp
mov rbp, rsp;
sub rsp, 32
and rsp, -16
mov rcx, dtitle
call printf
mov rcx, askparm
call printf
mov rcx, frmatin
mov rdx, a
mov r8, b
call scanf
movsd xmm0, [a]
movsd xmm1, [b]
pxor xmm2, xmm2
cmpeqsd xmm2, xmm0
movd eax, xmm2
test eax, eax
jnz notunique
pxor xmm2, xmm2
subsd xmm2, xmm1
divsd xmm2, xmm0
mov rcx, droots
movq rdx, xmm2
jmp done
notunique:
pxor xmm2, xmm2
cmpeqsd xmm2, xmm1
movd eax, xmm2
test eax, eax
jnz infsol
mov rcx, dnosol
jmp done
infsol:
mov rcx, dinfsol
done:
call printf
mov rsp, rbp
pop rbp
xor rax, rax
ret
The screenshot below shows the output of equation1.exe.
|
Sample 17: Equation of a line passing through two points.
The sample program equation2.asm determines the equation of a line passing through 2 points. The user is asked for the coefficients of the points A and B; the program determines the equation of the line (AB).
format ELF64
section '.data' writeable
askpt1 db "Coefficients x and y of point A? ", 0
askpt2 db "Coefficients x and y of point B? ", 0
frmatin db "%Lf%Lf", 0
line1 db "Equation of the line (AB): y = %.2fx + %.2f", 0Dh, 0Ah, 0
line1b db "Equation of the line (AB): y = %.2fx - %.2f", 0Dh, 0Ah, 0
line1c db "Equation of the line (AB): y = %.2f", 0Dh, 0Ah, 0
line2 db "Equation of the line (AB): x = %.2f", 0Dh, 0Ah, 0
section '.bss' writeable
x1 dq ?
y1 dq ?
x2 dq ?
y2 dq ?
section '.text' executable
public main
extrn printf
main:
push rbp
mov rbp, rsp;
sub rsp, 32
and rsp, -16
mov rcx, askpt1
call printf
mov rcx, frmatin
mov rdx, x1
mov r8, y1
call scanf
mov rcx, askpt2
call printf
mov rcx, frmatin
mov rdx, x2
mov r8, y2
call scanf
movsd xmm1, [x2]
subsd xmm1, [x1]
pxor xmm2, xmm2
cmpeqsd xmm2, xmm1
movd eax, xmm2
test eax, eax
jnz parallel_y
movsd xmm0, [y2]
subsd xmm0, [y1]
divsd xmm0, xmm1
pxor xmm2, xmm2
cmpeqsd xmm2, xmm0
movd eax, xmm2
test eax, eax
jnz parallel_x
movsd xmm3, xmm0
mulsd xmm0, [x1]
movsd xmm1, [y1]
subsd xmm1, xmm0
movq rdx, xmm3
pxor xmm2, xmm2
cmplesd xmm2, xmm1
movd eax, xmm2
test eax, eax
jz negative_oy
movq r8, xmm1
mov rcx, line1
jmp eq_print
negative_oy:
pxor xmm2, xmm2
subsd xmm2, xmm1
movq r8, xmm2
mov rcx, line1b
jmp eq_print
parallel_x:
movq rdx, xmm1
mov rcx, line1c
jmp eq_print
parallel_y:
movsd xmm0, [x1]
movq rdx, xmm0
mov rcx, line2
eq_print:
call printf
mov rsp, rbp
pop rbp
xor rax, rax
ret
The screenshot below shows the output of equation2.exe.
|
If you find this text helpful, please, support me and this website by signing my guestbook.